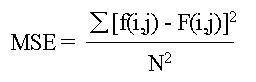libsquish (a popular DXT encoding library) internally uses a total ordering based method to find high-quality DXT endpoints. This method can also be applied to ETC1 encoding, using the equations in rg_etc1's optimizer's remarks to solve for optimal subblock colors given each possible selector distribution in the total ordering and the current best intensity index and subblock color.
I don't actually compute the total ordering, I instead iterate over all selector distributions present in the total ordering because the actual per-pixel selector values don't matter to the solver. So basically, the new optimizer first tries the subblock's average color, then it computes and tries a series of "correction" factors (relative to the subblock's average color), which depend on the current intensity table index and the current best subblock color found so far (to account for clamping). A hash table is also used to prevent the optimizer from evaluating a trial solution more than once.
Single threaded results:
perceptual: 0 etc2: 0 rec709: 1
Source filename: kodak\kodim03.png 768x512
--- basislib Quality: 4
basislib time: 5.644
basislib ETC image Error: Max: 70, Mean: 1.952, MSE: 8.220, RMSE: 2.867, PSNR: 38.982, SSIM: 0.964853
--- etc2comp effort: 100
etc2comp time: 75.792851
etc2comp Error: Max: 75, Mean: 1.925, MSE: 8.009, RMSE: 2.830, PSNR: 39.095, SSIM: 0.965339
--- etcpak time: 0.006
etcpak Error: Max: 80, Mean: 2.492, MSE: 12.757, RMSE: 3.572, PSNR: 37.073, SSIM: 0.944697
--- ispc_etc time: 1.021655
ispc_etc1 Error: Max: 75, Mean: 1.965, MSE: 8.280, RMSE: 2.877, PSNR: 38.951, SSIM: 0.963916
After enabling multithreading (40 threads) in those encoders that support it:
J:\dev\basislib1\bin>texexp kodak\kodim03.png
perceptual: 0 etc2: 0 rec709: 1
Source filename: kodak\kodim03.png 768x512
--- basislib Quality: 4
basislib pack time: 0.266
basislib ETC image Error: Max: 70, Mean: 1.952, MSE: 8.220, RMSE: 2.867, PSNR: 38.982, SSIM: 0.964853
--- etc2comp effort: 100
etc2comp time: 3.608819
etc2comp Error: Max: 75, Mean: 1.925, MSE: 8.009, RMSE: 2.830, PSNR: 39.095, SSIM: 0.965339
--- etcpak time: 0.006
etcpak Error: Max: 80, Mean: 2.492, MSE: 12.757, RMSE: 3.572, PSNR: 37.073, SSIM: 0.944697
--- ispc_etc time: 1.054324
ispc_etc1 Error: Max: 75, Mean: 1.965, MSE: 8.280, RMSE: 2.877, PSNR: 38.951, SSIM: 0.963916
Intel is doing some kind of amazing SIMD dark magic in there. The ETC1 cluster fit method is around 10-27x faster than rg_etc1 (which uses my previous method, a hybrid of a 3D neighborhood search with iterative base color refinement) and etc2comp (effort 100) in ETC1 mode. RGB Avg. PSNR is usually within ~.1 dB of Intel.
I'm so tempted to update rg_etc1 with this algorithm, if only I had the time.
Update 10/1: Okay, I computed a histogram of the "winning" subblock average color correction factors applied over a few hundred test textures. I then selected the top 64 correction factors (out of 165), and don't bother trying the rest. Here's a graph showing the usage histogram of the selector distributions across all the test textures, sorted by frequency (the most successfully selector distributions are to the right).
This works well in my testing, for another 2.25 - 5x speedup (depending on the # of factors you choose to apply):
J:\dev\basislib1\bin>texexp kodak\kodim03.png
perceptual: 0 etc2: 0 rec709: 1
Source filename: kodak\kodim03.png 768x512
--- basislib Quality: 4
basislib pack time: 0.118
basislib ETC image Error: Max: 70, Mean: 1.960, MSE: 8.276, RMSE: 2.877, PSNR: 38.953, SSIM: 0.964881
--- etc2comp effort: 100
etc2comp time: 3.621138
etc2comp Error: Max: 75, Mean: 1.925, MSE: 8.009, RMSE: 2.830, PSNR: 39.095, SSIM: 0.965339
--- etcpak time: 0.006
etcpak Error: Max: 80, Mean: 2.492, MSE: 12.757, RMSE: 3.572, PSNR: 37.073, SSIM: 0.944697
--- ispc_etc time: 1.038211
ispc_etc1 Error: Max: 75, Mean: 1.965, MSE: 8.280, RMSE: 2.877, PSNR: 38.951, SSIM: 0.963916
How It Works
Here's the basic math, from the comments:
// Now we have the input block, the avg. color of the input pixels, a set of trial selector indices, and the block color+intensity index.
// Now, for each component, attempt to refine the current solution by solving a simple linear equation. For example, for 4 pixels:
// The goal is:
// pixel0 - (block_color+inten_table[selector0]) + pixel1 - (block_color+inten_table[selector1]) + pixel2 - (block_color+inten_table[selector2]) + pixel3 - (block_color+inten_table[selector3]) = 0
// Rearranging this:
// (pixel0 + pixel1 + pixel2 + pixel3) - (block_color+inten_table[selector0]) - (block_color+inten_table[selector1]) - (block_color+inten_table[selector2]) - (block_color+inten_table[selector3]) = 0
// (pixel0 + pixel1 + pixel2 + pixel3) - block_color - inten_table[selector0] - block_color-inten_table[selector1] - block_color-inten_table[selector2] - block_color-inten_table[selector3] = 0
// (pixel0 + pixel1 + pixel2 + pixel3) - 4*block_color - inten_table[selector0] - inten_table[selector1] - inten_table[selector2] - inten_table[selector3] = 0
// (pixel0 + pixel1 + pixel2 + pixel3) - 4*block_color - (inten_table[selector0] + inten_table[selector1] + inten_table[selector2] + inten_table[selector3]) = 0
// (pixel0 + pixel1 + pixel2 + pixel3)/4 - block_color - (inten_table[selector0] + inten_table[selector1] + inten_table[selector2] + inten_table[selector3])/4 = 0
// block_color = (pixel0 + pixel1 + pixel2 + pixel3)/4 - (inten_table[selector0] + inten_table[selector1] + inten_table[selector2] + inten_table[selector3])/4
// So what this means:
// optimal_block_color = avg_input - avg_inten_delta
// So the optimal block color can be computed by taking the average block color and subtracting the current average of the intensity delta.
// Unfortunately, optimal_block_color must then be quantized to 555 or 444 so it's not always possible to improve matters using this formula.
// Also, the above formula is for unclamped intensity deltas. The actual implementation takes into account clamping.
To implement cluster fit for ETC1, you can iterate over the total ordering of all the selectors for each of the 8 subblock pixels, much like squish does in DXT1. However, doing this is unnecessary, because all that ultimately matters in the refinement equation is the computed avg_inten_delta, which just depends on the selector distribution (and not what each pixel's selector actually is).
Here's my current optimizer's compute() function. It first tries the subblock's average color (at coordinates m_br, m_bg, m_bb), to establish a baseline (minimally useful) solution, then it iterates over the precomputed (and sorted) selector distribution table and attempts applying (usually) a few dozen or so avg. color "correction" factors from this table. The table is sorted, so the entries with the highest probability of applying the best correction appear first (as mentioned above).
Note that evaluate_solution() uses a hash table to avoid trying the same solution more than once. The sorted table of total ordering selector distributions is at the bottom of this post.
// total_perms_to_try: 1-64 seems good enough (out of 165)
void etc1_optimizer::compute_internal_cluster_fit_fast(uint total_perms_to_try)
{
if ((!m_best_solution.m_valid) || ((m_br != m_best_solution.m_coords.m_unscaled_color.r) || (m_bg != m_best_solution.m_coords.m_unscaled_color.g) || (m_bb != m_best_solution.m_coords.m_unscaled_color.b)))
{
evaluate_solution(etc1_solution_coordinates(m_br, m_bg, m_bb, 0, m_pParams->m_use_color4), m_trial_solution, &m_best_solution);
}
if ((m_best_solution.m_error == 0) || (!m_best_solution.m_valid))
return;
for (uint i = 0; i < total_perms_to_try; i++)
{
int delta_sum_r = 0, delta_sum_g = 0, delta_sum_b = 0;
const int *pInten_table = g_etc1_inten_tables[m_best_solution.m_coords.m_inten_table];
const color_quad_u8 base_color(m_best_solution.m_coords.get_scaled_color());
const uint8 *pNum_selectors = g_cluster_fit_order_tab[i].m_v;
for (uint q = 0; q < 4; q++)
{
const int yd_temp = pInten_table[q];
delta_sum_r += pNum_selectors[q] * (math::clamp<int>(base_color.r + yd_temp, 0, 255) - base_color.r);
delta_sum_g += pNum_selectors[q] * (math::clamp<int>(base_color.g + yd_temp, 0, 255) - base_color.g);
delta_sum_b += pNum_selectors[q] * (math::clamp<int>(base_color.b + yd_temp, 0, 255) - base_color.b);
}
if ((!delta_sum_r) && (!delta_sum_g) && (!delta_sum_b))
continue;
const float avg_delta_r_f = static_cast<float>(delta_sum_r) / 8;
const float avg_delta_g_f = static_cast<float>(delta_sum_g) / 8;
const float avg_delta_b_f = static_cast<float>(delta_sum_b) / 8;
const int br1 = math::clamp<int>(static_cast<uint>((m_avg_color[0] - avg_delta_r_f) * m_limit / 255.0f + .5f), 0, m_limit);
const int bg1 = math::clamp<int>(static_cast<uint>((m_avg_color[1] - avg_delta_g_f) * m_limit / 255.0f + .5f), 0, m_limit);
const int bb1 = math::clamp<int>(static_cast<uint>((m_avg_color[2] - avg_delta_b_f) * m_limit / 255.0f + .5f), 0, m_limit);
#if BASISLIB_DEBUG_ETC_ENCODER_DEEPER
printf("Second refinement trial %u, avg_delta %f %f %f\n", refinement_trial, avg_delta_r_f, avg_delta_g_f, avg_delta_b_f);
#endif
evaluate_solution(etc1_solution_coordinates(br1, bg1, bb1, 0, m_pParams->m_use_color4), m_trial_solution, &m_best_solution);
if (m_best_solution.m_error == 0)
break;
}
}
const uint BASISLIB_CLUSTER_FIT_ORDER_TABLE_SIZE = 165;
static const struct { uint8 m_v[4]; } g_cluster_fit_order_tab[BASISLIB_CLUSTER_FIT_ORDER_TABLE_SIZE] =
{
{ 0, 0, 0, 8 }, { 0, 5, 2, 1 }, { 0, 6, 1, 1 }, { 0, 7, 0, 1 }, { 0, 7, 1, 0 },
{ 0, 0, 8, 0 }, { 0, 0, 3, 5 }, { 0, 1, 7, 0 }, { 0, 0, 4, 4 }, { 0, 0, 2, 6 },
{ 0, 0, 7, 1 }, { 0, 0, 1, 7 }, { 0, 0, 5, 3 }, { 1, 6, 0, 1 }, { 0, 0, 6, 2 },
{ 0, 2, 6, 0 }, { 2, 4, 2, 0 }, { 0, 3, 5, 0 }, { 3, 3, 1, 1 }, { 4, 2, 0, 2 },
{ 1, 5, 2, 0 }, { 0, 5, 3, 0 }, { 0, 6, 2, 0 }, { 2, 4, 1, 1 }, { 5, 1, 0, 2 },
{ 6, 1, 1, 0 }, { 3, 3, 0, 2 }, { 6, 0, 0, 2 }, { 0, 8, 0, 0 }, { 6, 1, 0, 1 },
{ 0, 1, 6, 1 }, { 1, 6, 1, 0 }, { 4, 1, 3, 0 }, { 0, 2, 5, 1 }, { 5, 0, 3, 0 },
{ 5, 3, 0, 0 }, { 0, 1, 5, 2 }, { 0, 3, 4, 1 }, { 2, 5, 1, 0 }, { 1, 7, 0, 0 },
{ 0, 1, 4, 3 }, { 6, 0, 2, 0 }, { 0, 4, 4, 0 }, { 2, 6, 0, 0 }, { 0, 2, 4, 2 },
{ 0, 5, 1, 2 }, { 0, 6, 0, 2 }, { 3, 5, 0, 0 }, { 0, 4, 3, 1 }, { 3, 4, 1, 0 },
{ 4, 3, 1, 0 }, { 1, 5, 0, 2 }, { 0, 3, 3, 2 }, { 1, 4, 1, 2 }, { 0, 4, 2, 2 },
{ 2, 3, 3, 0 }, { 4, 4, 0, 0 }, { 1, 2, 4, 1 }, { 0, 5, 0, 3 }, { 0, 1, 3, 4 },
{ 1, 5, 1, 1 }, { 1, 4, 2, 1 }, { 1, 3, 2, 2 }, { 5, 2, 1, 0 }, { 1, 3, 3, 1 },
{ 0, 1, 2, 5 }, { 1, 1, 5, 1 }, { 0, 3, 2, 3 }, { 2, 5, 0, 1 }, { 3, 2, 2, 1 },
{ 2, 3, 0, 3 }, { 1, 4, 3, 0 }, { 2, 2, 1, 3 }, { 6, 2, 0, 0 }, { 1, 0, 6, 1 },
{ 3, 3, 2, 0 }, { 7, 1, 0, 0 }, { 3, 1, 4, 0 }, { 0, 2, 3, 3 }, { 0, 4, 1, 3 },
{ 0, 4, 0, 4 }, { 0, 1, 0, 7 }, { 2, 0, 5, 1 }, { 2, 0, 4, 2 }, { 3, 0, 2, 3 },
{ 2, 2, 4, 0 }, { 2, 2, 3, 1 }, { 4, 0, 3, 1 }, { 3, 2, 3, 0 }, { 2, 3, 2, 1 },
{ 1, 3, 4, 0 }, { 7, 0, 1, 0 }, { 3, 0, 4, 1 }, { 1, 0, 5, 2 }, { 8, 0, 0, 0 },
{ 3, 0, 1, 4 }, { 4, 1, 1, 2 }, { 4, 0, 2, 2 }, { 1, 2, 5, 0 }, { 4, 2, 1, 1 },
{ 3, 4, 0, 1 }, { 2, 0, 3, 3 }, { 5, 0, 1, 2 }, { 5, 0, 0, 3 }, { 2, 4, 0, 2 },
{ 2, 1, 4, 1 }, { 4, 0, 1, 3 }, { 2, 1, 5, 0 }, { 4, 2, 2, 0 }, { 4, 0, 4, 0 },
{ 1, 0, 4, 3 }, { 1, 4, 0, 3 }, { 3, 0, 3, 2 }, { 4, 3, 0, 1 }, { 0, 1, 1, 6 },
{ 1, 3, 1, 3 }, { 0, 2, 2, 4 }, { 2, 0, 2, 4 }, { 5, 1, 1, 1 }, { 3, 0, 5, 0 },
{ 2, 3, 1, 2 }, { 3, 0, 0, 5 }, { 0, 3, 1, 4 }, { 5, 0, 2, 1 }, { 2, 1, 3, 2 },
{ 2, 0, 6, 0 }, { 3, 1, 3, 1 }, { 5, 1, 2, 0 }, { 1, 0, 3, 4 }, { 1, 1, 6, 0 },
{ 4, 0, 0, 4 }, { 2, 0, 1, 5 }, { 0, 3, 0, 5 }, { 1, 3, 0, 4 }, { 4, 1, 2, 1 },
{ 1, 2, 3, 2 }, { 3, 1, 0, 4 }, { 5, 2, 0, 1 }, { 1, 2, 2, 3 }, { 3, 2, 1, 2 },
{ 2, 2, 2, 2 }, { 6, 0, 1, 1 }, { 1, 2, 1, 4 }, { 1, 1, 4, 2 }, { 3, 2, 0, 3 },
{ 1, 2, 0, 5 }, { 1, 0, 7, 0 }, { 3, 1, 2, 2 }, { 1, 0, 2, 5 }, { 2, 0, 0, 6 },
{ 2, 1, 1, 4 }, { 2, 2, 0, 4 }, { 1, 1, 3, 3 }, { 7, 0, 0, 1 }, { 1, 0, 0, 7 },
{ 2, 1, 2, 3 }, { 4, 1, 0, 3 }, { 3, 1, 1, 3 }, { 1, 1, 2, 4 }, { 2, 1, 0, 5 },
{ 1, 0, 1, 6 }, { 0, 2, 1, 5 }, { 0, 2, 0, 6 }, { 1, 1, 1, 5 }, { 1, 1, 0, 6 }
};